DeepLearning2 その1

January 31, 2021

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装が稀に見る良書だったので、ゼロから作るDeep Learning ❷ ―自然言語処理編を購入しました。これからこちらを読んでいきます。

第1章ニューラルネットワークの復習

数学とpythonの復習

要素の演算

単純な足し算

>>> import numpy as np
>>> W = np.array([[1, 2, 3], [4, 5, 6]])
>>> X = np.array([[0, 1, 2], [3, 4, 5]])
>>> W + X
array([[ 1,  3,  5],
       [ 7,  9, 11]])
>>>

ブロードキャスト

>>> A = np.array([[1, 2], [3, 4]])
>>> A * 10
array([[10, 20],
       [30, 40]])
>>> b = np.array([10, 20])
>>> A * b
array([[10, 40],
       [30, 80]])
>>>

次元がちがう配列も賢く計算されています。

ベクトルの内積

x=(x1, x2, …, xn), y=(y1, y2, …, yn)の二つのベクトルがあった時、対応する要素の積を足し合わせたものがベクトルの内積となります。

xとyの内積

x・y = x1y1 + x2y2 + ... + xnyn

numpyでは内積をdotで計算します。

>>> a = np.array([1, 2, 3])
>>> b = np.array([4, 5, 6])
>>> np.dot(a, b)
32
>>> 1 * 4 + 2 * 5 + 3 * 6
32
>>>

また、dotは行列の積にも使います。

>>> A = np.array([[1, 2], [3, 4]])
>>> B = np.array([[5, 6], [7, 8]])
>>> np.dot(A, B)
array([[19, 22],
       [43, 50]])
>>> [[1 * 5 + 2 * 7, 1 * 6 + 2 * 8], [3 * 5 + 4 * 7, 3 * 6 + 4 * 8]]
[[19, 22], [43, 50]]
>>>

Numpy exercise 100というのもあるらしい。ただ、numpyに詳しくなりたいわけではないので先に進みます。

行列の形状

行列の積を行うには対応する次元の要素数を合わせる必要があます。
Aの行列が3 x 2の行列場合、積を行う要素は2 x Nである必要があります。
行列の形状はshapeで確認できます。

>>> a = np.array([[1, 2], [1, 2], [1, 2,]])
>>> a.shape
(3, 2)
>>> b = np.array([[1, 2, 3], [1, 2, 3]])
>>> b.shape
(2, 3)
>>> np.dot(a, b)  # (3, 2)と(2, 3)は隣り合う要素数が一致するのでOK
array([[3, 6, 9],
       [3, 6, 9],
       [3, 6, 9]])
>>> b = np.array([[1, 2, 3, 4], [1, 2, 3, 4]])
>>> b.shape
(2, 4)
>>> np.dot(a, b)  # (3, 2)と(2, 4)は隣り合う要素数が一致するのでOK
array([[ 3,  6,  9, 12],
       [ 3,  6,  9, 12],
       [ 3,  6,  9, 12]])
>>> b = np.array([[1, 2], [1, 2], [1, 2]])
>>> b.shape
(3, 2)
>>> np.dot(a, b)  # (3, 2)と(3, 2)は隣り合う要素数が一致しないのでNG
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<__array_function__ internals>", line 6, in dot
ValueError: shapes (3,2) and (3,2) not aligned: 2 (dim 1) != 3 (dim 0)
>>>

ニューラルネットワークの推論

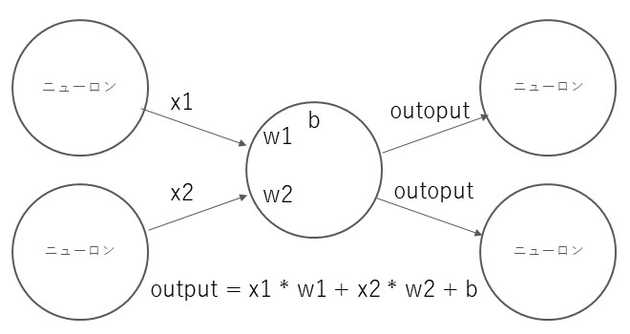
ニューラルネットワークは複数のニューロンの組み合わせから成り立ちます。ニューロンとは、前段のニューロンから送られてくる値に重みをかけたものを足し、定数(バイアス)を加えたものを次のニューロンに送る存在です。

入力の行列(列ベクトル)をx、重みの行列をW、バイアスをbとすると、出力hは以下の式のようになります

h = xW + b

入力x1, x2に対する重みを2, 4、バイアスを4としてpythonで計算すると以下のようになります。

>>> W = np.array([2, 4])
>>> b = np.array([4])
>>> np.dot(x, W) + b
array([44])
>>> 2 * 10 + 4 * 5 + 4
44
>>>

第1章 ニューラルネットワークの復習